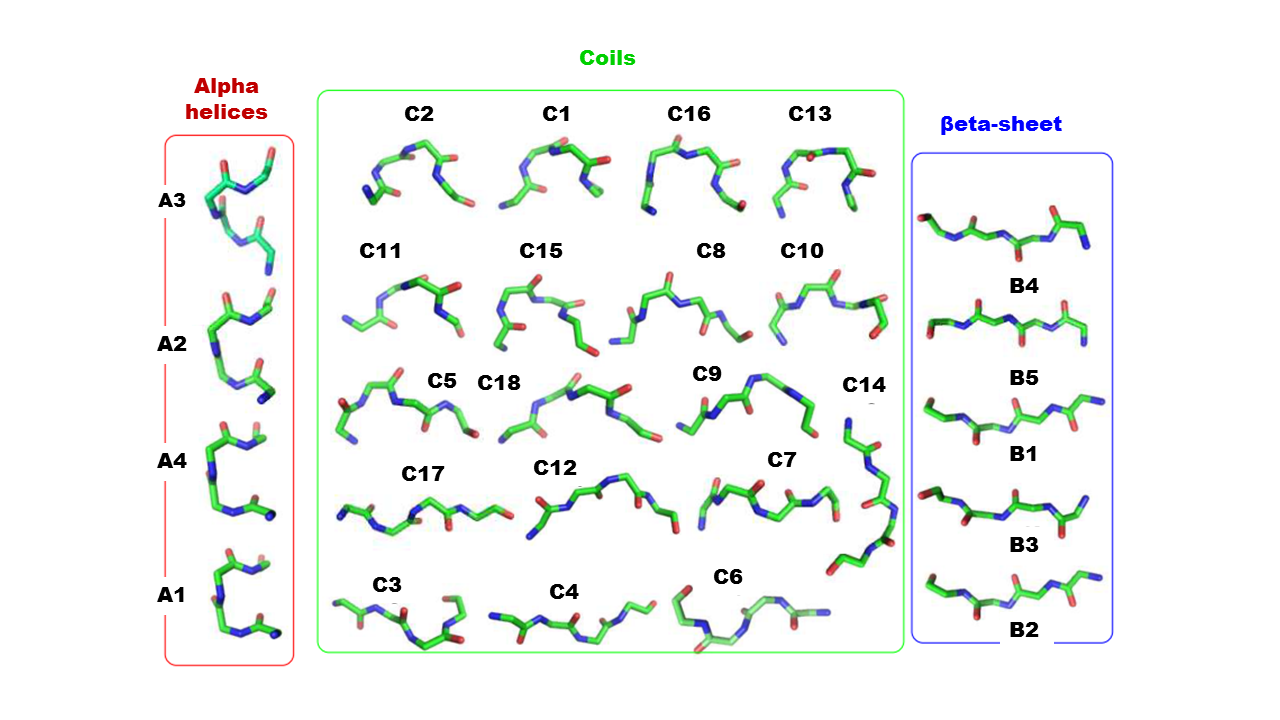
Structural letter A1
$$ μ_{A1}=
\begin{pmatrix}
5.43 & 5.09 & 5.42 & 2.94 \\
\end{pmatrix}
$$
$$ Σ_{A1}=
\begin{pmatrix}
0.007 & 0.005 & 0 & -0.002 \\
0.005 & 0.022 & 0.003 & 0.014 \\
0 & 0.003 & 0.007 & -0.004 \\
-0.002 & 0.014 & -0.004 & 0.023 \\
\end{pmatrix}
$$
$$ μ_{A2}=
\begin{pmatrix}
5.41 & 5.23 & 5.61 & 2.86 \\
\end{pmatrix}
$$
$$ Σ_{A2}=
\begin{pmatrix}
0.011 & 0.01 & -0 & -0.003 \\
0.01 & 0.037 & 0.004 & 0.026 \\
-0 & 0.004 & 0.006 & -0.004 \\
-0.003 & 0.026 & -0.004 & 0.041 \\
\end{pmatrix}
$$
$$ μ_{A3}=
\begin{pmatrix}
5.62 & 5.25 & 5.42 & 2.87 \\
\end{pmatrix}
$$
$$ Σ_{A3}=
\begin{pmatrix}
0.008 & 0.008 & 0 & -0.001 \\
0.008 & 0.039 & 0.007 & 0.027 \\
0 & 0.007 & 0.011 & -0.007 \\
-0.001 & 0.027 & -0.007 & 0.044 \\
\end{pmatrix}
$$
$$ μ_{A4}=
\begin{pmatrix}
5.39 & 5.09 & 5.38 & 2.92 \\
\end{pmatrix}
$$
$$ Σ_{A4}=
\begin{pmatrix}
0.031 & 0.015 & -0.011 & -0.008 \\
0.015 & 0.06 & 0.01 & 0.033 \\
-0.011 & 0.01 & 0.03 & -0.011 \\
-0.008 & 0.033 & -0.011 & 0.062 \\
\end{pmatrix}
$$
$$ μ_{B1}=
\begin{pmatrix}
6.87 & 10.06 & 6.51 & -1.41 \\
\end{pmatrix}
$$
$$ Σ_{B1}=
\begin{pmatrix}
0.062 & 0.06 & 0.039 & -0.028 \\
0.06 & 0.1 & 0.082 & 0.021 \\
0.039 & 0.082 & 0.078 & 0.001 \\
-0.028 & 0.021 & 0.001 & 0.257 \\
\end{pmatrix}
$$
$$ μ_{B2}=
\begin{pmatrix}
6.71 & 9.64 & 6.5 & -2.6 \\
\end{pmatrix}
$$
$$ Σ_{B2}=
\begin{pmatrix}
0.101 & 0.076 & 0.02 & -0.03 \\
0.076 & 0.114 & 0.064 & 0.044 \\
0.02 & 0.064 & 0.061 & 0.033 \\
-0.03 & 0.044 & 0.033 & 0.117 \\
\end{pmatrix}
$$
$$ μ_{B3}=
\begin{pmatrix}
6.39 & 9.93 & 6.75 & -1.07 \\
\end{pmatrix}
$$
$$ Σ_{B3}=
\begin{pmatrix}
0.05 & 0.047 & 0.017 & -0.01 \\
0.047 & 0.063 & 0.04 & 0.038 \\
0.017 & 0.04 & 0.047 & 0.027 \\
-0.01 & 0.038 & 0.027 & 0.253 \\
\end{pmatrix}
$$
$$ μ_{B4}=
\begin{pmatrix}
6.48 & 10.17 & 7.09 & 0.66 \\
\end{pmatrix}
$$
$$ Σ_{B4}=
\begin{pmatrix}
0.084 & 0.076 & 0.013 & 0.045 \\
0.076 & 0.076 & 0.017 & 0.008 \\
0.013 & 0.017 & 0.022 & 0.011 \\
0.045 & 0.008 & 0.011 & 0.306 \\
\end{pmatrix}
$$
$$ μ_{B5}=
\begin{pmatrix}
6.8 & 10.35 & 6.85 & -0.25 \\
\end{pmatrix}
$$
$$ Σ_{B5}=
\begin{pmatrix}
0.055 & 0.056 & 0.03 & -0.001 \\
0.056 & 0.07 & 0.051 & 0.009 \\
0.03 & 0.051 & 0.048 & 0.009 \\
-0.001 & 0.009 & 0.009 & 0.198 \\
\end{pmatrix}
$$
$$ μ_{C1}=
\begin{pmatrix}
5.4 & 5.58 & 5.42 & 3.39 \\
\end{pmatrix}
$$
$$ Σ_{C1}=
\begin{pmatrix}
0.022 & 0.016 & -0.002 & -0.002 \\
0.016 & 0.063 & 0.006 & 0.028 \\
-0.002 & 0.006 & 0.019 & -0.008 \\
-0.002 & 0.028 & -0.008 & 0.027 \\
\end{pmatrix}
$$
$$ μ_{C2}=
\begin{pmatrix}
5.59 & 5.49 & 5.78 & 2.58 \\
\end{pmatrix}
$$
$$ Σ_{C2}=
\begin{pmatrix}
0.054 & 0.056 & -0.017 & 0.018 \\
0.056 & 0.194 & 0.034 & 0.111 \\
-0.017 & 0.034 & 0.045 & -0.01 \\
0.018 & 0.111 & -0.01 & 0.155 \\
\end{pmatrix}
$$
$$ μ_{C3}=
\begin{pmatrix}
6.57 & 8.96 & 5.58 & -2.19 \\
\end{pmatrix}
$$
$$ Σ_{C3}=
\begin{pmatrix}
0.141 & 0.056 & 0.018 & -0.082 \\
0.056 & 0.1 & 0.062 & 0.072 \\
0.018 & 0.062 & 0.062 & -0.003 \\
-0.082 & 0.072 & -0.003 & 0.442 \\
\end{pmatrix}
$$
$$ μ_{C4}=
\begin{pmatrix}
6.72 & 9.12 & 6.41 & -3.31 \\
\end{pmatrix}
$$
$$ Σ_{C4}=
\begin{pmatrix}
0.1 & 0.076 & 0.001 & -0.01 \\
0.076 & 0.13 & 0.044 & 0.043 \\
0.001 & 0.044 & 0.047 & 0.033 \\
-0.01 & 0.043 & 0.033 & 0.042 \\
\end{pmatrix}
$$
$$ μ_{C5}=
\begin{pmatrix}
5.66 & 8.07 & 6.7 & 2.96 \\
\end{pmatrix}
$$
$$ Σ_{C5}=
\begin{pmatrix}
0.076 & 0.087 & 0.006 & -0.01 \\
0.087 & 0.319 & 0.072 & -0.089 \\
0.006 & 0.072 & 0.091 & -0.109 \\
-0.01 & -0.089 & -0.109 & 0.159 \\
\end{pmatrix}
$$
$$ μ_{C6}=
\begin{pmatrix}
6.21 & 9.21 & 5.77 & 0.27 \\
\end{pmatrix}
$$
$$ Σ_{C6}=
\begin{pmatrix}
0.146 & 0.107 & 0.037 & -0.022 \\
0.107 & 0.124 & 0.086 & -0.006 \\
0.037 & 0.086 & 0.089 & 0.033 \\
-0.022 & -0.006 & 0.033 & 0.571 \\
\end{pmatrix}
$$
$$ μ_{C7}=
\begin{pmatrix}
5.66 & 8.95 & 6.54 & 2.09 \\
\end{pmatrix}
$$
$$ Σ_{C7}=
\begin{pmatrix}
0.058 & 0.049 & -0.001 & 0.007 \\
0.049 & 0.097 & 0.027 & -0.127 \\
-0.001 & 0.027 & 0.076 & -0.023 \\
0.007 & -0.127 & -0.023 & 0.399 \\
\end{pmatrix}
$$
$$ μ_{C8}=
\begin{pmatrix}
5.7 & 7.26 & 7.02 & 0.88 \\
\end{pmatrix}
$$
$$ Σ_{C8}=
\begin{pmatrix}
0.075 & 0.131 & 0.013 & -0.01 \\
0.131 & 0.4 & 0.098 & -0.059 \\
0.013 & 0.098 & 0.047 & -0.096 \\
-0.01 & -0.059 & -0.096 & 1.074 \\
\end{pmatrix}
$$
$$ μ_{C9}=
\begin{pmatrix}
6.71 & 8.27 & 5.47 & -3.56 \\
\end{pmatrix}
$$
$$ Σ_{C9}=
\begin{pmatrix}
0.09 & 0.027 & -0.005 & -0.026 \\
0.027 & 0.09 & 0.035 & 0.03 \\
-0.005 & 0.035 & 0.039 & 0.001 \\
-0.026 & 0.03 & 0.001 & 0.042 \\
\end{pmatrix}
$$
$$ μ_{C10}=
\begin{pmatrix}
5.55 & 7.74 & 5.6 & -3.31 \\
\end{pmatrix}
$$
$$ Σ_{C10}=
\begin{pmatrix}
0.06 & 0.04 & -0.01 & -0.001 \\
0.04 & 0.131 & -0.009 & 0.108 \\
-0.01 & -0.009 & 0.049 & -0.028 \\
-0.001 & 0.108 & -0.028 & 0.144 \\
\end{pmatrix}
$$
$$ μ_{C11}=
\begin{pmatrix}
5.6 & 6.71 & 5.58 & 3.69 \\
\end{pmatrix}
$$
$$ Σ_{C11}=
\begin{pmatrix}
0.083 & 0.117 & 0.026 & -0 \\
0.117 & 0.362 & 0.103 & 0.014 \\
0.026 & 0.103 & 0.08 & -0.009 \\
-0 & 0.014 & -0.009 & 0.01 \\
\end{pmatrix}
$$
$$ μ_{C12}=
\begin{pmatrix}
6.89 & 8.94 & 6.76 & -0.48 \\
\end{pmatrix}
$$
$$ Σ_{C12}=
\begin{pmatrix}
0.086 & 0.097 & -0.023 & -0.172 \\
0.097 & 0.839 & 0.252 & 0.063 \\
-0.023 & 0.252 & 0.135 & 0.171 \\
-0.172 & 0.063 & 0.171 & 3.735 \\
\end{pmatrix}
$$
$$ μ_{C13}=
\begin{pmatrix}
6.47 & 5.92 & 5.56 & 0.53 \\
\end{pmatrix}
$$
$$ Σ_{C13}=
\begin{pmatrix}
0.1 & 0.183 & 0.001 & 0.029 \\
0.183 & 0.449 & 0.062 & 0.202 \\
0.001 & 0.062 & 0.039 & 0.036 \\
0.029 & 0.202 & 0.036 & 1.305 \\
\end{pmatrix}
$$
$$ μ_{C14}=
\begin{pmatrix}
6.87 & 8.28 & 6.03 & -3.44 \\
\end{pmatrix}
$$
$$ Σ_{C14}=
\begin{pmatrix}
0.074 & 0.05 & -0.029 & -0.007 \\
0.05 & 0.28 & 0.148 & 0.026 \\
-0.029 & 0.148 & 0.156 & 0.064 \\
-0.007 & 0.026 & 0.064 & 0.069 \\
\end{pmatrix}
$$
$$ μ_{C15}=
\begin{pmatrix}
6.03 & 6.85 & 5.64 & -0.63 \\
\end{pmatrix}
$$
$$ Σ_{C15}=
\begin{pmatrix}
0.442 & 0.499 & -0.016 & 0.431 \\
0.499 & 1.869 & 0.23 & 0.789 \\
-0.016 & 0.23 & 0.221 & -0.113 \\
0.431 & 0.789 & -0.113 & 6.57 \\
\end{pmatrix}
$$
$$ μ_{C16}=
\begin{pmatrix}
5.78 & 5.68 & 6.07 & 1.46 \\
\end{pmatrix}
$$
$$ Σ_{C16}=
\begin{pmatrix}
0.075 & 0.094 & -0.015 & 0.023 \\
0.094 & 0.256 & 0.062 & 0.058 \\
-0.015 & 0.062 & 0.061 & -0.044 \\
0.023 & 0.058 & -0.044 & 0.363 \\
\end{pmatrix}
$$
$$ μ_{C17}=
\begin{pmatrix}
5.66 & 8.91 & 6.66 & -1.46 \\
\end{pmatrix}
$$
$$ Σ_{C17}=
\begin{pmatrix}
0.118 & 0.097 & 0.024 & -0.04 \\
0.097 & 0.276 & -0.021 & 0.287 \\
0.024 & -0.021 & 0.138 & -0.082 \\
-0.04 & 0.287 & -0.082 & 1.15 \\
\end{pmatrix}
$$
$$ μ_{C18}=
\begin{pmatrix}
5.69 & 8.09 & 5.67 & 3.09 \\
\end{pmatrix}
$$
$$ Σ_{C18}=
\begin{pmatrix}
0.055 & 0.034 & 0 & 0.01 \\
0.034 & 0.141 & 0.044 & -0.128 \\
0 & 0.044 & 0.07 & 0.003 \\
0.01 & -0.128 & 0.003 & 0.217 \\
\end{pmatrix}
$$